Iverson bracket
In mathematics, the Iverson bracket, named after Kenneth E. Iverson, is a notation that denotes a number that is 1 if the condition in square brackets is satisfied, and 0 otherwise. More exactly,
where P is a statement that can be true or false. This notation was introduced by Kenneth E. Iverson in his programming language APL,[1] while the specific restriction to square brackets was advocated by Donald Knuth to avoid ambiguity in parenthesized logical expressions.[2]
Contents |
Uses
The notation is useful in expressing sums or integrals without boundary conditions. For example
In the first sum, the index  is limited to be in the range 1 to 10. The second sum is allowed to range over all integers, but where i is strictly less than 1 or strictly greater than 10, the summand is 0, contributing nothing to the sum. Such use of the Iverson bracket can permit easier manipulation of these expressions.
is limited to be in the range 1 to 10. The second sum is allowed to range over all integers, but where i is strictly less than 1 or strictly greater than 10, the summand is 0, contributing nothing to the sum. Such use of the Iverson bracket can permit easier manipulation of these expressions.
Another use of the Iverson bracket is to simplify equations with special cases. For example, the formula
(a number-theoretic identity involving the Euler phi function) which is valid only for 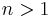 may be written
may be written
which is valid for all positive integers n.
Special cases
The Kronecker delta notation is a specific case of Iverson notation when the condition is equality. That is,
The indicator function, another specific case, has set membership as its condition:
The sign function and Heaviside step function are also easily expressed in this notation:
And the trichotomy of the reals can be expressed:
Notes
- ^ Ronald Graham, Donald Knuth, and Oren Patashnik. Concrete Mathematics, Section 2.2: Sums and Recurrences.
- ^ Knuth 1992.
References
- Donald Knuth, "Two Notes on Notation", American Mathematical Monthly, Volume 99, Number 5, May 1992, pp. 403–422. (TeX, arXiv:math/9205211)
- Kenneth E. Iverson, A Programming Language, New York: Wiley, p. 11, 1962.
![[P] = \begin{cases} 1 & \mbox{if } P \mbox{ is true;} \\ 0 & \mbox{otherwise.} \end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/eca574431fff8c9b2a555bcc9c8cfba8.png)
![\sum_{1\le i \le 10} i^2 = \sum_{i} i^2[1 \le i \le 10].](/2012-wikipedia_en_all_nopic_01_2012/I/20d4a5cee25b06e98a36e173b1022a5d.png)
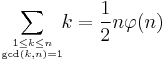
![\sum_{1\le k\le n \atop (k,n)=1}\!\!k = \frac{1}{2}n(\varphi(n)%2B[n=1])](/2012-wikipedia_en_all_nopic_01_2012/I/4d983636b8c48b6795d61004438aede8.png)
![\delta_{ij} = [i=j].\,](/2012-wikipedia_en_all_nopic_01_2012/I/b17d8699b618ec6e77e5d14234f9cdb3.png)
![\mathbf{I}_A(x) = [x\in A].](/2012-wikipedia_en_all_nopic_01_2012/I/18a8a7f57b1dd9694c366442041be2de.png)
![\sgn(x) = [x > 0] - [x < 0]](/2012-wikipedia_en_all_nopic_01_2012/I/a81835d92a2534037a9a9dc2cd0afd38.png)
![H(x) = [x > 0] %2B \frac{1}{2}[x=0].](/2012-wikipedia_en_all_nopic_01_2012/I/0abe32ed2acc26cca6de49b550837695.png)
![[a < b] %2B [a = b] %2B [a > b] = 1.](/2012-wikipedia_en_all_nopic_01_2012/I/469e49869d6ece37eb2510daaa6d81b5.png)